Алгоритмы — это пошаговые инструкции решения задач

Одним из фундаментальных понятий в информатике является понятие алгоритма. Происхождение самого термина «алгоритм» связано с математикой. Это слово происходит от Algorithmi — латинского написания имени Мухаммеда аль-Хорезми (783–850), выдающегося математика средневекового Востока. В XII в. был выполнен латинский перевод его математического трактата, из которого европейцы узнали о десятичной позиционной системе счисления и правилах арифметики многозначных чисел. Именно эти правила в то время называли алгоритмами. Сложение, вычитание, умножение столбиком, деление уголком многозначных чисел — вот первые алгоритмы в математике.

В наше время понятие алгоритма трактуется шире. Алгоритм — это последовательность команд управления каким-либо исполнителем.

Исполнитель — это тот, для кого составляют правила и план, тот, кто будет их выполнять. Это человек, животное, или машина, которые понимают и умеют точно исполнять отдаваемые им команды.

Команда — это указание исполнителю совершить некоторое действие.

Для каждого исполнителя определена система команд — т.е. набор команд, которые он может выполнить. У разных исполнителей разные системы команд.

В рамках науки термин (понятие) «алгоритм» относится к категории неопределяемых понятий, т.е. не обладающих формальным определением в терминах более простых понятий. Содержание неопределяемого понятия раскрывают: при помощи описаний применения понятия (поясняют на примерах); путем сопоставления данного понятия с содержанием других понятий. Цель публикации — раскрыть содержание понятия «алгоритм».

Алгоритмы окружают человека во всех сферах деятельности и в повседневной жизни. Как перейти дорогу, как дойти до магазина, как найти на карте города Торговый Центр, как решить математическое уравнение, как получить необходимые сведения по какому-либо вопросу и пр. — все строится по алгоритму.

Таким образом, алгоритм может быть предназначен для его выполнения человеком или автоматическим устройством — формальным исполнителем. Задача исполнителя — точная реализация уже имеющегося алгоритма. Формальный исполнитель не обязан вникать в сущность алгоритма, а возможно, и неспособен его понять.

Примером формального исполнителя может служить автоматическая стиральная машина, которая неукоснительно исполняет предписанные ей действия, даже если вы забыли положить в нее порошок. Человек тоже может выступать в роли формального исполнителя, но в первую очередь формальными исполнителями являются различные автоматические устройства, и компьютер в том числе.

Можно выделить алгоритмы вычислительные и управляющие

Вычислительный алгоритм, одно из основных понятий вычислительной математики, последовательность действий, которая, начиная с заданных исходных данных, за конечное число шагов приводит к искомому результату.

Блок-схема циклического алгоритма управления

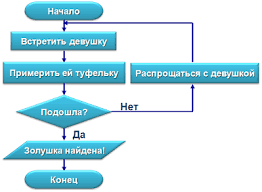
Простейшими примерами вычислительного алгоритма являются правила сложения, вычитания, умножения и деления. Под вычислительным алгоритмом часто также понимают последовательность инструкций (последовательность арифметических действий и условных операторов), которые могут быть однозначным образом реализованы в виде программы на компьютере. Вычислительные алгоритмы, по сути, преобразуют некоторые начальные данные в выходные, реализуя вычисление некоторой функции.

Алгоритм управления — это последовательность команд по управлению объектом, приводящая к заранее поставленной цели.

Семантика управляющих алгоритмов существенным образом может отличаться и сводиться к выдаче необходимых управляющих воздействий либо в заданные моменты времени, либо в качестве реакции на внешние события (в этом случае, в отличие от вычислительного алгоритма, управляющий может оставаться корректным при бесконечном выполнении).

Циклический алгоритм управления с постусловием, его блок-схема

Далее речь идёт о вычислительных алгоритмах

Работа по решению любой задачи с использованием компьютера (исполнителя) делится на следующие этапы:

Постановка задачи.
Формализация задачи.
Построение алгоритма.
Составление программы на языке программирования.
Отладка и тестирование программы.
Использование программы.

Часто эту последовательность называют технологической цепочкой решения задачи. Непосредственно к программированию в этом списке относятся пункты 3, 4, 5.

На этапе постановки задачи должно быть четко сформулировано, что дано и что требуется найти. Здесь очень важно определить полный набор исходных данных, необходимых для получения решения.

Второй этап — формализация задачи. Здесь чаще всего задача переводится на язык математических формул, уравнений, отношений. Если решение требует математического описания какого-то реального объекта, явления или процесса, то формализация равносильна получению соответствующей математической модели.

Третий этап — построение алгоритма. Процесс разработки алгоритма для решения задачи называется алгоритмизацией.

Алгоритмизация играет важную роль в информатике и программировании, так как хорошо разработанные алгоритмы обеспечивают эффективное и корректное выполнение задач, а также упрощают процесс отладки и поддержки программного кода.

Первые три этапа предусматривают работу без компьютера. Дальше следует собственно программирование на определенном языке, в определенной системе программирования. Последний (шестой) этап — это использование уже разработанной программы в практических целях.

Таким образом, программист должен обладать следующими знаниями и навыками:

уметь строить алгоритмы;
знать языки программирования;
уметь работать в соответствующей системе программирования.

Свойства алгоритма

Понятность — инструкции, используемые в алгоритме, должны быть понятны исполнителю, т.е. алгоритм должен включать только действия (команды), известные исполнителю.

Дискретность (прерывность, раздельность) — алгоритм должен представлять процесс решения задачи как последовательное выполнение простых шагов. Каждое действие, предусмотренное алгоритмом, исполняется только после того, как закончилось исполнение предыдущего.

Определенность (детерминированность) — предполагает получение однозначного результата вычислительного процecca при заданных исходных данных. Благодаря этому свойству процесс выполнения алгоритма носит механический характер. Для этого на каждом шаге алгоритма не должно возникать разночтений и разногласий, т.е. инструкции должны быть четко определены.

Завершаемость (конечность) — алгоритм должен приводить к решению задачи за конечное число шагов, т.е. алгоритмы конечны, они должны завершаться и выдавать результат за заранее известное число шагов.

Результативность — завершение алгоритма определенным результатом, т.е. выполнение алгоритма должно привести к какому-либо результату и не оставлять неопределенности. Результат может в том числе оказаться неудачным — например, алгоритм может сообщить, что решения нет!

Массовость — алгоритм решения задачи разрабатывается в общем виде, т.е. он должен быть применим для некоторого класса задач, различающихся только исходными данными. При этом исходные данные могут выбираться из некоторой области, которая называется областью применимости алгоритма. Например, стандартный алгоритм по решению квадратного уравнения останется неизменным вне зависимости от того, какие числа будут использоваться в этом уравнении.

Классификация алгоритмов

Несмотря на слово «последовательность», алгоритм не всегда описывает действия в жестко заданном порядке. Особенно это актуально сейчас, с распространением асинхронности в программировании. Существует несколько классификаций алгоритмов. Как было сказано ранее алгоритмы делятся на две большие группы: вычислительные алгоритмы и управляющие алгоритмы. Есть особые алгоритмы управления, в которых цикл управления может быть бесконечным.

Вычислительные алгоритмы в зависимости от порядка действий исполнителя подразделяются следующим образом:

Линейный алгоритм — набор команд (инструкций), выполняемых последовательно во времени друг за другом. Они не переставляются местами, не повторяются, выполняются при любых условиях.
Разветвляющийся алгоритм — алгоритм, содержащий хотя бы одно условие, в результате проверки которого может осуществляться разделение на несколько параллельных ветвей алгоритма.
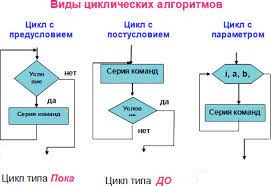Циклический алгоритм — алгоритм, предусматривающий многократное повторение одного и того же действия (одних и тех же операций) над новыми исходными данными. Цикл программы — последовательность команд (тело цикла), которая может выполняться многократно (для новых исходных данных) до удовлетворения некоторого условия: например, повторять этот блок команд, пока в структуре данных не останется пустых ячеек. К циклическим алгоритмам сводится большинство методов вычислений, перебора вариантов.
1. Цикл с предусловием (Цикл типа Пока)
2. Цикл с постусловием (Цикл типа До)
3. Цикл с параметром
Рекурсивный алгоритм: Рекурсия — это явление, когда какой-то алгоритм вызывает сам себя, но с другими входными данными. Это не цикл: данные другие, но «экземпляров» работающих программ несколько, а не одна. Известный пример рекурсивного алгоритма — расчет чисел Фибоначчи.

Таким образом в алгоритмах есть место для условий, циклов и других нелинейных конструкций.

Основные и вспомогательные. Это еще один вид классификации. Основной алгоритм решает непосредственную задачу, вспомогательный решает подзадачу и может использоваться внутри основного — для этого там просто указываются его название и входные данные. Пример вспомогательного алгоритма — любая программная функция.

Формы записи алгоритмов

На практике наиболее распространены следующие формы представления алгоритмов:

словесная (запись на естественном языке)
словесно-формульная (задание инструкций с использованием математических символов и выражений в сочетании со словесными пояснениями)
графическая (изображения из графических символов)
псевдокоды (полуформализованные описания алгоритмов на условном алгоритмическом языке, включающие в себя как элементы языка программирования, так и фразы естественного языка, общепринятые математические обозначения и др.
программная (тексты на языках программирования)

Пример: написать алгоритм «Одеться по погоде». Если на улице температура ниже −8, то необходимо надеть шубу, иначе — пальто.

Словесный способ записи алгоритма

Словесный способ записи алгоритмов представляет собой описание последовательных этапов обработки данных. Алгоритм задается на естественном языке в произвольной форме с требуемой детализацией.

Пример 1. Алгоритм ПОГОДА
Начало
определить температуру воздуха
если температура ниже −8, то надеть шубу, иначе надеть пальто
Конец

Словесно-формульный способ записи алгоритма

Для исполнителя-человека алгоритм может быть представлен предложениями обычного текста с использованием в случае необходимости математической или другой символики. Такой способ записи алгоритма называют словесно-формульным.

Пример 2. Алгоритм поиска вещественных корней квадратного уравнения
ах² + Ьх + с = 0, a ≠ 0 :

Задать значения коэффициентов a, b и c.
Вычислить дискриминант D = b² − 4ac.
Проверить условие существования вещественных корней D ≥ 0.
Если D ≥ 0 выполнено, то перейти к шагу 5.
Если не выполнено (т.е. D < 0), то перейти к шагу 4.
Дать ответ – «вещественных корней нет». Перейти к шагу 8.
Проверить условие существования двух различных корней D > 0.
Если условие выполнено, то перейти к шагу 7,
иначе – перейти к шагу 6.
Вычислить корень уравнения x = -b/2a.
Дать ответ – «уравнение имеет один корень x».
Перейти к шагу 8.
Вычислить корни уравнения
х1 = (-b + √D)/2a,
х2 = (-b − √D)/2a.
Дать ответ – «уравнение имеет два корня x1, x2».
Закончить вычисления.

Словесный способ не имеет широкого распространения, так как такие описания:

строго не формализуемы;
страдают многословностью записей;
допускают неоднозначность толкования отдельных предписаний.

Графический способ записи алгоритмов

Наибольшее распространение благодаря своей наглядности получил графический способ записи алгоритмов. При графическом представлении алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий.

ГОСТ. Блок-схема циклического алгоритма управления

Схема циклического алгоритма с постусловием

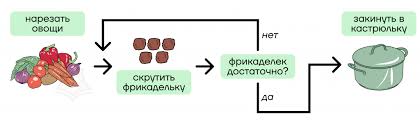
Такое графическое представление называется схемой алгоритма или блок-схемой. В блок-схеме каждому типу действий (вводу исходных данных, вычислению значений выражений, проверке условий, управлению повторением действий, окончанию обработки и т.п.) соответствует геометрическая фигура, представленная в виде блочного символа. Блочные символы соединяются линиями переходов, определяющими очередность выполнения действий. В таблице 1 приведены наиболее часто употребляемые символы.

ГОСТ 19.701-90, блочные символы для построения блок-схем алгоритмов

Таблица 1. Блочные символы для построения блок-схем алгоритмов

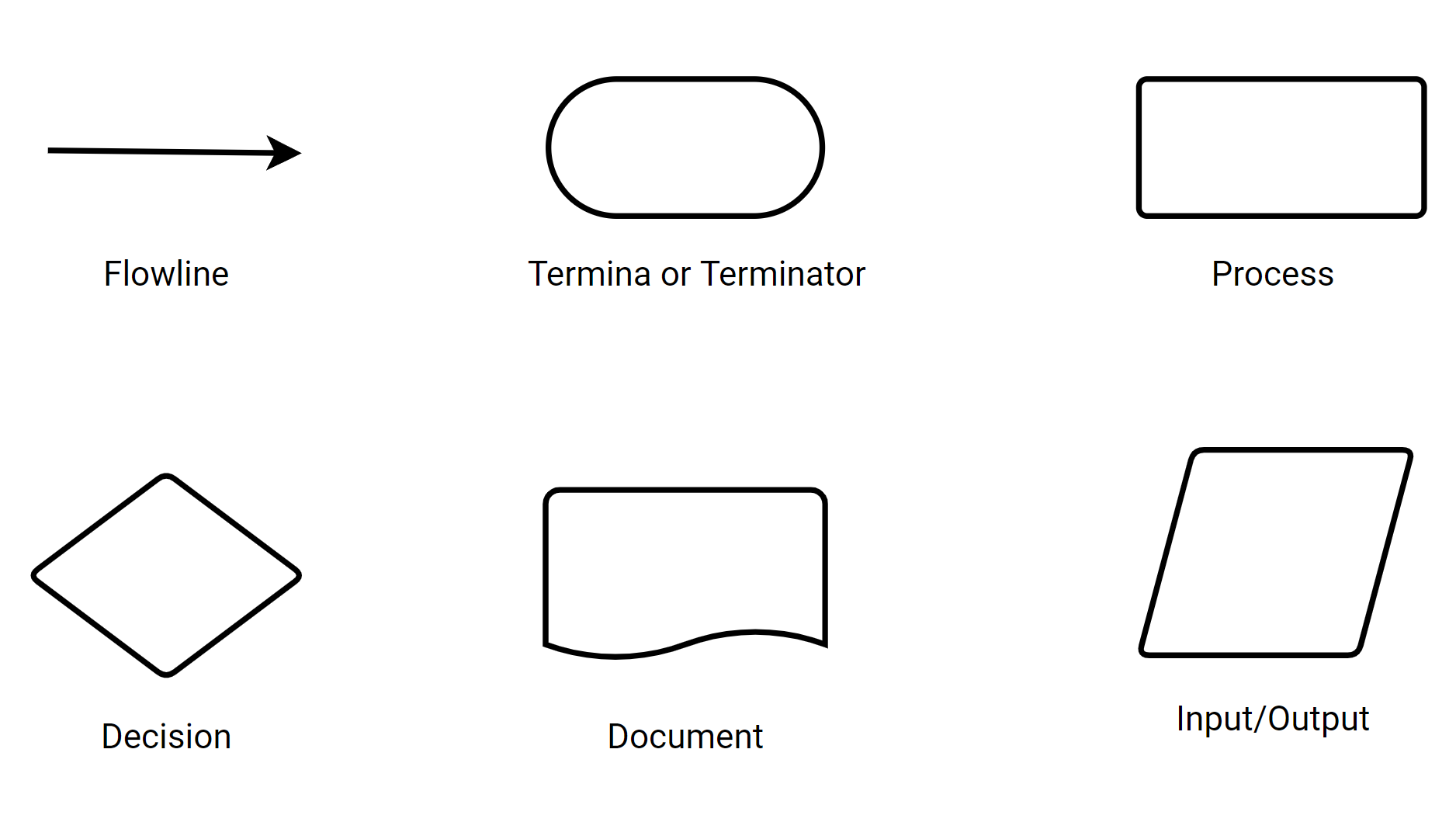
Flowline: Линия потока показывает направление процесса, соединяя два блока друг с другом.

Termina or Terminator: Терминал или терминатор представляет собой начальную или конечную точки процесса блок -схемы.

Process: Символ процесса является наиболее распространенным компонентом блок-схемы и указывает на шаг в процессе.

Decision: Этот символ представляет решение, которое вы или ваша команда должны принять, чтобы достичь следующего шага процесса. Как правило, это истинное или ложное решение или вопрос «да» или «нет», на который вам нужно ответить.

Document: Этот символ представляет единственный документ.

Input/Output: Символ ввода/вывода представляет процесс внедрения или вывода внешних данных.

Блок процесс (Process) применяется для обозначения действия или последовательности действий, изменяющих значение, форму представления или размещения данных. Для улучшения наглядности схемы несколько отдельных блоков обработки можно объединять в один блок. Представление отдельных операций достаточно свободно.

Блок решение (Decision) используется для обозначения переходов управления по условию. В каждом блоке решение должны быть указаны вопрос, условие или сравнение, которые он определяет.

Блок модификация используется для организации циклических конструкций. (Слово модификация означает видоизменение, преобразование). Внутри блока записывается параметр цикла, для которого указываются его начальное значение, граничное условие и шаг изменения значения параметра для каждого повторения.

Блок предопределенный процесс используется для указания обращений к вспомогательным алгоритмам, существующим автономно в виде некоторых самостоятельных модулей, и для обращений к библиотечным подпрограммам.

Блок Ввод-вывод (Input/Output) используется для преобразования данных в форму, пригодную для обработки (ввод) или отображения результатов обработки (вывод). Отдельным логическим устройствам компьютера или отдельным функциям обмена соответствуют определенные блочные символы. В каждом из них указываются тип устройства или файла данных, тип информации, участвующий в обмене, а также вид операции обмена.

Блок Пуск-останов (Termina or Terminator) используется для обозначения начала, конца, прерывания процесса обработки данных или выполнения программы.

Блок Документ (Document) предназначен для ввода-вывода данных, носителем которых служит бумага.

Внутри блока дается описание соответствующих действий. Блоки, как правило, располагаются сверху вниз. Линии соединения отдельных блоков показывают направление процесса обработки в схеме. Стрелки на соединяющих линиях не ставятся при направлениях сверху вниз и слева направо; противоположные направления показывают стрелкой на линии.

Другие фигуры блок-схем вы найдёте в документации к ГОСТ 19.701-90.

Уметь читать блок-схемы полезный навык, поэтому приведем несколько примеров блок-схем различных алгоритмов >>

Блок-схема алгоритма "Квадратное уравнение"

Рисунок: Блок-схема циклического алгоритма

Блок-схема рекурсивного алгоритма-процедуры

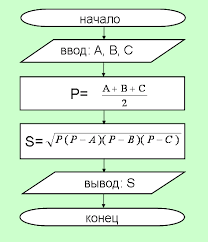
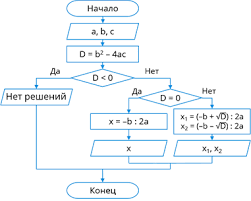
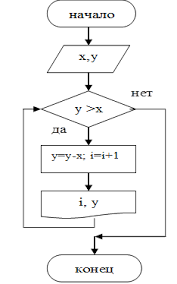
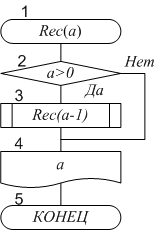
Рисунок 1. Примеры блок-схем вычислительных алгоритмов

Блок-схемы широко используются при написании программ, так как они:

Гораздо проще для понимания, чем запись в виде команд.
Упрощают процесс отладки.
Позволяют составить эффективную программную документацию.
Облегчают процесс демонстрации и обсуждения программы.

Псевдокод

Псевдокод представляет собой систему обозначений и правил, предназначенную для единообразной записи алгоритмов.

Псевдокод занимает промежуточное место между естественным и формальным языками. С одной стороны, он близок к обычному естественному языку, поэтому алгоритмы могут на нем записываться и читаться как обычный текст. С другой стороны, в псевдокоде используются некоторые формальные конструкции и математическая символика, что приближает запись алгоритма к общепринятой математической записи.

В псевдокоде не приняты строгие синтаксические правила для записи команд, присущие формальным языкам, что облегчает запись алгоритма на стадии его проектирования и дает возможность использовать более широкий набор команд, рассчитанный на абстрактного исполнителя.

Однако в псевдокоде обычно имеются некоторые конструкции, присущие формальным языкам, что облегчает переход от записи на псевдокоде к записи алгоритма на формальном языке. В частности, в псевдокоде, так же, как и в формальных языках, есть служебные слова, смысл которых определен раз и навсегда. Они выделяются в печатном тексте жирным шрифтом, а в рукописном тексте подчеркиваются.

Единого или формального определения псевдокода не существует, поэтому возможны различные псевдокоды, отличающиеся набором служебных слов и основных (базовых) конструкций.

Программный способ записи алгоритмов

При записи алгоритма в словесной форме, в виде блок-схемы или на псевдокоде допускается определенный произвол при изображении команд. Вместе с тем такая запись точна настолько, что позволяет человеку понять суть дела и исполнить алгоритм.

Однако на практике в качестве исполнителей алгоритмов используются специальные автоматы — компьютеры. Поэтому алгоритм, предназначенный для исполнения на компьютере, должен быть записан на понятном ему языке. И здесь на первый план выдвигается необходимость точной записи команд, не оставляющей места для произвольного толкования их исполнителем.

Следовательно, язык для записи алгоритмов должен быть формализован. Такой язык принято называть языком программирования, а запись алгоритма на этом языке — программой для компьютера.

Программа, создаваемая человеком — программистом, представляет собой текст, состоящий из знаков, как правило букв, цифр и специальных знаков. Знаки в тексте программы часто объединены в последовательности - ключевые слова, слова объединены в предложения языка программирования — операторы. Каждый оператор, как правило, записывается в отдельную строку текста программы.

Таким образом текстовое программирование представляет собой иерархическую последовательность знаков, слов, операторов, записываемых и читаемых последовательно, как обычный писменный текст.


//Пример программы на языке C#
namespace oap
{
class Program
{
static void Main(string[] args)
{
var string mess;
Console.WriteLine("введите
   температуру воздуха t: ");
var t = int.Parse(
         Console.ReadLine());
if (t < -8)
{
 mess = "Одеть шубу";
else
 mess = "Одеть пальто";
}
Console.WriteLine(mess);
}}}

Общие принципы построения алгоритмов

При разработке алгоритма используют следующие основные принципы.

Принцип поэтапной детализации алгоритма (другое название — «проектирование сверху-вниз»). Этот принцип предполагает первоначальную разработку алгоритма в виде укрупненных блоков (разбиение задачи на подзадачи) и их постепенную детализацию.

Принцип «от главного к второстепенному», предполагающий составление алгоритма, начиная с главной конструкции. При этом, часто, приходится «достраивать» алгоритм в обратную сторону, например, от середины к началу.

Принцип структурирования, т.е. использования только типовых алгоритмических структур при построении алгоритма. Нетиповой структурой считается, например, циклическая конструкция, содержащая в теле цикла дополнительные выходы из цикла. В программировании нетиповые структуры появляются в результате злоупотребления командой безусловного перехода (GoTo). При этом программа хуже читается и труднее отлаживается.

Сложность алгоритма

Понятие «сложность» — одно из ключевых в изучении алгоритмов. Оно означает не то, насколько трудно понять тот или иной способ решения задачи (конкретный алгоритм), а ресурсы, затраченные на решение задачи данным способом (алгоритмом).

Существует несколько способов измерения сложности алгоритма. Программисты обычно сосредотачивают внимание на скорости алгоритма, но не менее важны и другие показатели — требования к объёму памяти, свободному месте на диске. Использование быстрого алгоритма не приведёт к ожидаемым результатам, если для его работы понадобится больше памяти, чем есть у компьютера.

Сложность алгоритма обычно описывают большой латинской буквой O. После нее в скобках указывается значение, от которого зависит время выполнения данного алгоритма, т.е. это временная сложность алгоритма.

Повествование о понятии «сложность алгоритма» выходит за рамки данной статьи, так как этот навык (оценка сложности алгоритма) необходим только программистам. На наш взгляд Адитья Бхаргава в своей книге «Грокаем алгоритмы» удачно нашел слова и иллюстрации для рассказа об этом сложном понятии, мы её рекомендуем для изучения всем, кто заинтересован в расширении своих знаний по данной теме.

Понятие алгоритма